Spatial Differences

Simple Example

If you subtract a polygon that is partially inside another polygon, it is easy to visually imagine what you will get - a polygon, a multipolygon. Example Code and diagram below.

SELECT 1 As gid, g.geom1, g.geom2, ST_Difference(g.geom1, g.geom2) As diff_geom12, 
ST_Difference(g.geom2, g.geom1) As diff_geom21, 
ST_SymDifference(g.geom1,g.geom2) As diff_symgeom12
INTO diftest
FROM (SELECT ST_Buffer(ST_MakePoint(9,3),2) As geom1, 
    ST_Buffer(ST_MakePoint(10,2),1) As geom2) As g;

Geom1 and Geom2 overlaid on top of each other
Geom1 - Geom2 (ST_Difference(geom1,geom2))	Geom2 - Geom1 (ST_Difference(geom2,geom1))
(ST_SymDifference(geom1,geom2)) - note this is equivalent to ST_SymDifference(geom2,geom1)

What happens when you subtract a line from a polygon that runs thru the polygon?

The result of this in PostGIS surprised me a bit and I think it is wrong, but I'm not sure there is a right answer. I'm not absolutely sure what it should be but just that PostGIS seems to be wrong. To be honest I'm not sure if such a thing has an agreeable visual meaning. To the naked eye what PostGIS returns looks like the original polygon and is still a polygon but it is not the same polygon and placing this under a magnifying glass (the difference between the original polygon and the new one is empty, but the difference between new polygon and the original is some sort of multipolygon thing - which if you think about it is absolutely ridiculous - its like saying your world has gotten slightly bigger by removal of a line). At first I thought what should it return? Should it bisect it or maybe the polygon would just fall apart into a glob of points or lines or maybe it would just be the same polygon.

What exactly does it mean to subtract out something that has no area from an area? I have no idea. I know what it means from a mathematical sense - It is the range of points that defines the polygon excluding the range of points that defines the line and if you think about mathematical limits you can see the various parts of the polygon ebbing about the line but never touching it. Unfortunately things possible in calculus just seem to fall apart at the fringes when you try to stuff them into a model that thinks in boundary absolutes and are also hard to visualize when you try to apply normal visual terminology to them. Note the range of points that defines a line is infinite just as the range of points that defines the polygon is infinite, but the polygon is an area range (composed of an infinite number of lines) and the line is a linear range (composed of an infinite number of points).

• You can throw out the becomes a blob of points or lines because if it did it wouldn't be infinite anymore and infinity - 1 is still infinity
• But what about bisects it into 2 polygons? Haven't quite convinced myself that this is not possible because if the line goes right thru it why wouldn't it break into two polygons with each having a border that is an epsilon away from the line but the boundary not actually being the line? What concesssions would you need to make to represent this polygon side that can not be the line but is infinitesimally close to the line? You can assume its the line but then your whole (The polygon except the LINE argument falls apart at the fringes because now both polygons intersect the LINE). Shockingly even the differences you can visualize fall apart at the boundaries. If you take the above simple example - you will see that the new Polygons still intersect that part that was removed. That seems to violate set theory of differences. SELECT ST_Intersects(diff_geom12, geom2) as diffgeom12_intersects FROM diftest returns true

Below is some code and accompanying diagram for the line that cuts threw the polygon:

SELECT 1 As gid, g.geom1, g.geom2, ST_Difference(g.geom1, g.geom2) As diff_geom12, 
ST_Difference(g.geom2, g.geom1) As diff_geom21, ST_SymDifference(g.geom1,g.geom2) As diff_symgeom12
INTO diftest2
FROM (SELECT ST_Buffer(ST_MakePoint(9,3),2) As geom1, 
    ST_MakeLine(ST_MakePoint(8,0), ST_MakePoint(10,9)) As geom2) As g;

Below are some simple tests to inspect

SELECT ST_Area(geom1) = ST_Area(diff_geom12) As is_areasame, 
    St_AsBinary(geom1) = St_AsBinary(diff_geom12) As binary_equal, 
        ST_Equals(geom1,diff_geom12)  As spatially_equal,
    ST_GeometryType(geom1) As geom1_type, 
    ST_GeometryType(diff_geom12) As geom12_type
FROM diftest2;

 is_areasame | binary_equal | spatially_equal | geom1_type | geom12_type
-------------+--------------+-----------------+------------+-------------
 t           | f            | f               | ST_Polygon | ST_Polygon

And if we ask how are they different:

SELECT 
    ST_AsText(ST_Difference(geom1,diff_geom12)) As diff_geom1_geom12,
   ST_GeometryType(ST_Difference(diff_geom12,geom1)) As diff_geom12_geom1
FROM diftest2;

    diff_geom1_geom12     | diff_geom12_geom1
--------------------------+-------------------
 GEOMETRYCOLLECTION EMPTY | ST_MultiPolygon

The magical increase in size of our polygon is caused by those black things.
Yes those black things are polygons forming the multipolygon - that mysterious polygon that got added to our original polygon when we subtracted the line from our polygon.
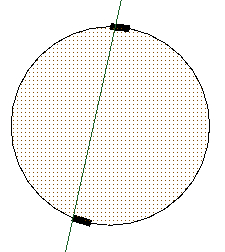
. Yes you ask a nonsensical question and you get a ludicrous answer.

Now if you subtract a polygon from a line, and the polygon runs thru the line, then the line no longer has that piece that resided in the polygon and may break into two lines (a MULTILINESTRING) so that is fairly comforting visually although mathematically it is still unappealing at the fringes.

This all reminds me of reading a blind programmer's writings and he said something to the effect I pity those sighted programmers; they have difficulty programming in more than 2 dimensions because their perception of depth is clouded by their vision.. After reading that I realized he was right and my over-reliance on vision cripples my ability to think beyond what I can see. It made me appreciate just how easily one skill can drown out the others and that it is probably not desirable to sit back idly and allow this to happen. This whole topic of differences also makes me think of this xkcd comic on reading braille
.